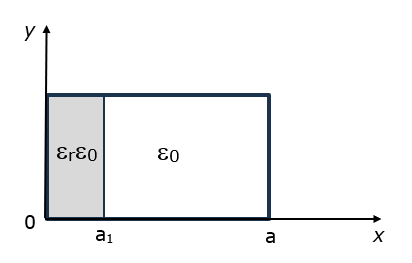
SS-V：9003 2つの材料を持つ共振器

テスト番号VE04 2つの材料を持つ共振器のモード解析

定義

Figure 1.


モデルの詳細：
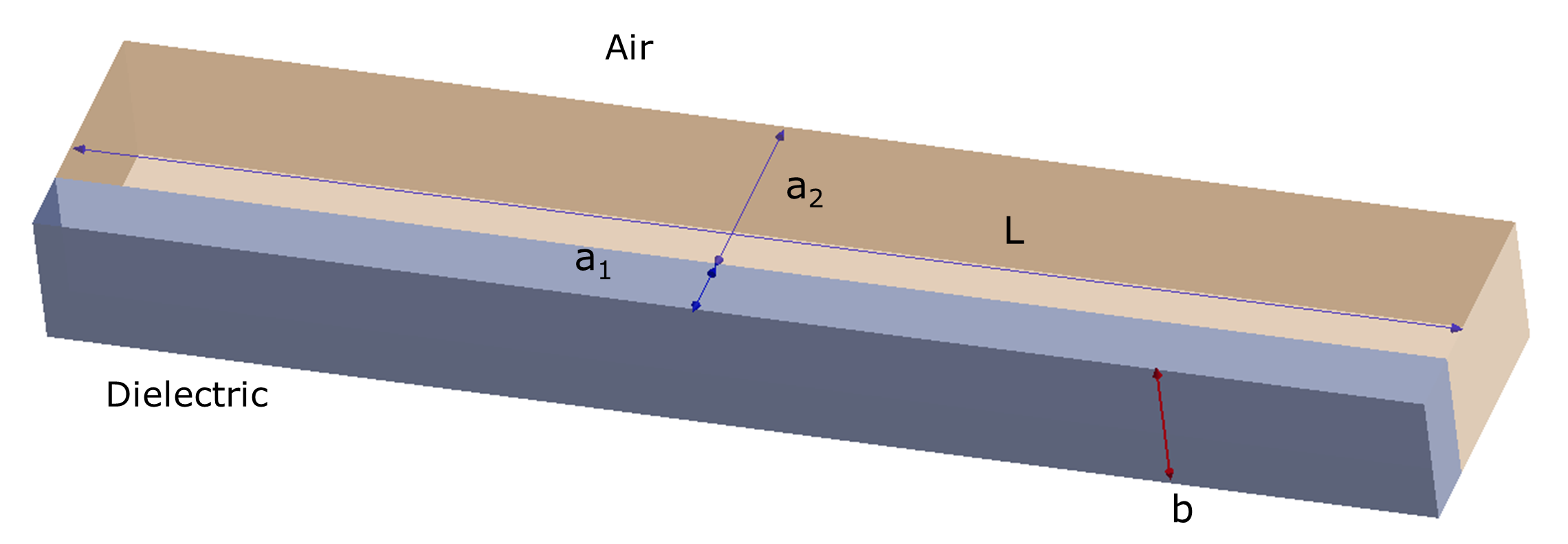
  • 図 1：a1 = 5mm、a2 = 15mm、a = a1 + a2、b = 10 mm、L = 100 mm
  • すべての壁面はPEC（完全電気導体）条件下となります
材料特性は以下のとおりです。
特性
値
誘電体の比誘電率（ ε r ）
4.0
誘電体の比透磁率（ μ r ）
1.0
空気の比透磁率（ ε r ）
1.0
空気の比透磁率（ μ r ）
1.0

基準解

Figure 2. 共振器の断面


ここでは、 T E 10 l モード（l=1を持つモードが基本モード）を求めます。これはy1への依存性がないことを意味します。

縦磁場の方程式は次のようになります。

∂ 2 ∂ x 2 + k D 2 H z = 0     for     0 ≤ x ≤ a 1
∂ 2 ∂ x 2 + k A 2 H z = 0     for     a 1 ≤ x ≤ a
ここで、
k A 2 =   k 0 2 - πl L 2
および
k D 2 =   ε r k 0 2 - πl L 2

モデルパラメータの組み合わせによって、 k A 2 と k D 2 の両方が正、または k D 2 が正で k A 2 は負になります。

最初のケースの k 0 の値は次の方程式の解から得られます。

k A tan k D a 1 + k D tan k A a 2 = 0

これは上記1の定義に基づいて、 k A 2 と k D 2 を代入したものです。

k A 2 が負の値の場合、同様の方法で、 β の値が方程式の解から得られます（このケースは、Pozarの1のケースを補完）。

k A tan k D a 1 + k D tan h k A a 2 = 0
ここで、
k A 2 = -   k A 2 = - k 0 2 + πl L 2
およびこれは正です。

これらの超越方程式の根は、必要な精度に応じて、数値的またはグラフ的に求めることができます。

1つ目のケースの電場の分布は以下のようになります。
Figure 3.


2つ目のケースの電場の分布は以下のようになります。
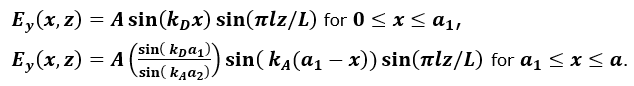
Figure 4.


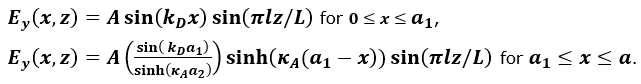
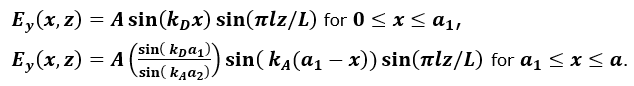
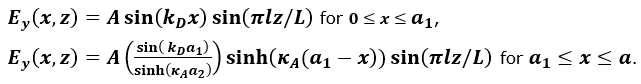
結果

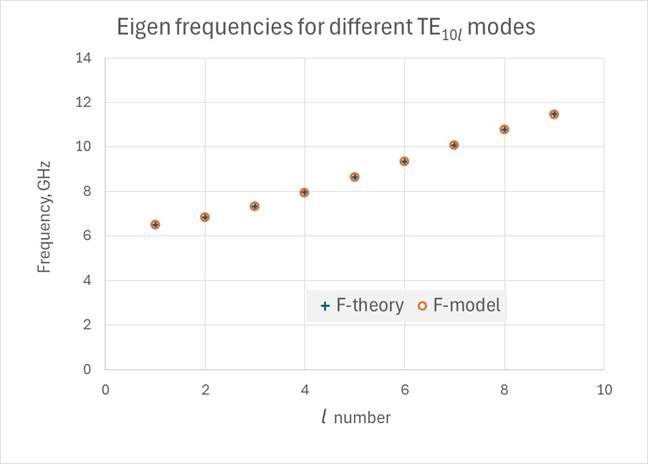
T E 10 l のモードの理論上の共振周波数、およびモデリングで得られた共振周波数の比較を、以下の図に示します
Figure 5. 理論上の共振周波数とモデルの共振周波数の比較


場のz依存性は単純で、解の中で非常に正確に考慮されます。x依存性のモデルでの再現がどの程度正確なのかを確認するのは興味深いことです。電界強度は、その最大値の1つに対応する固定のzで出力され、その最大値に合わせて正規化されます。以下に、l=3のケースについてこれを示します。
Figure 6. T E 103 モードの電界強度 E X , Z の分布


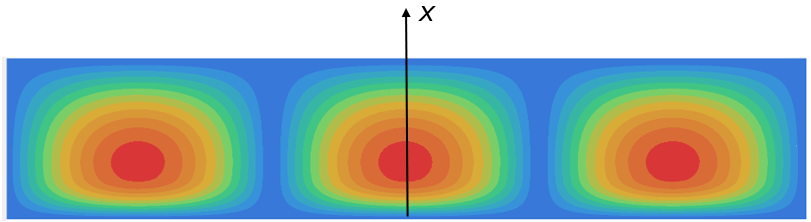
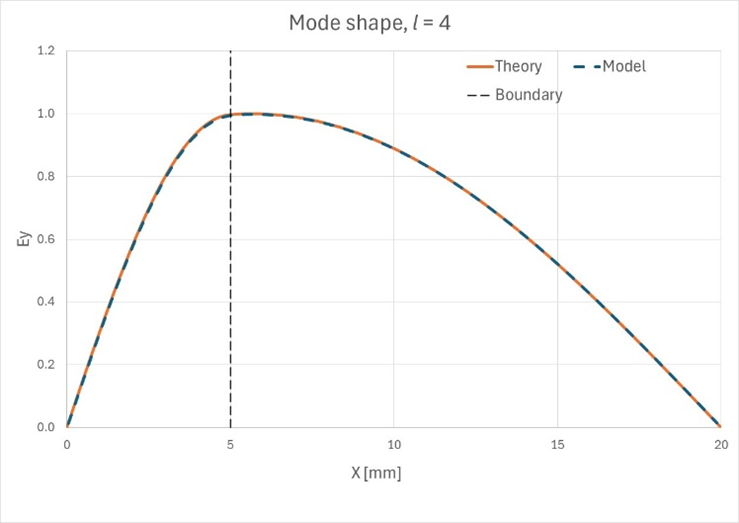
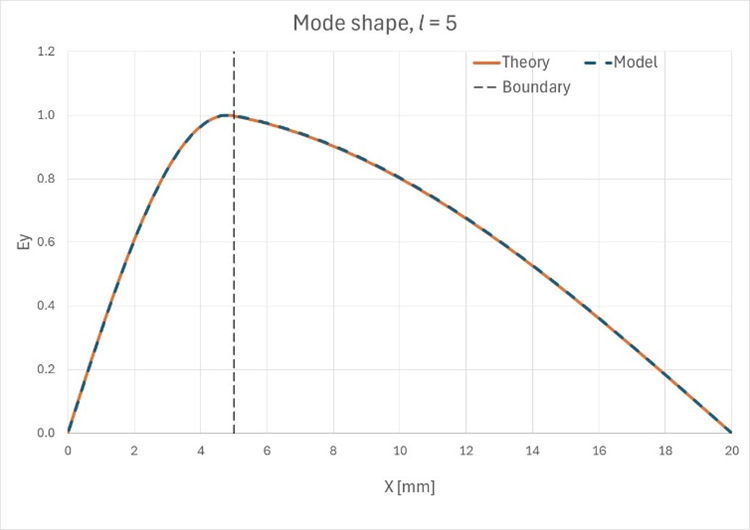
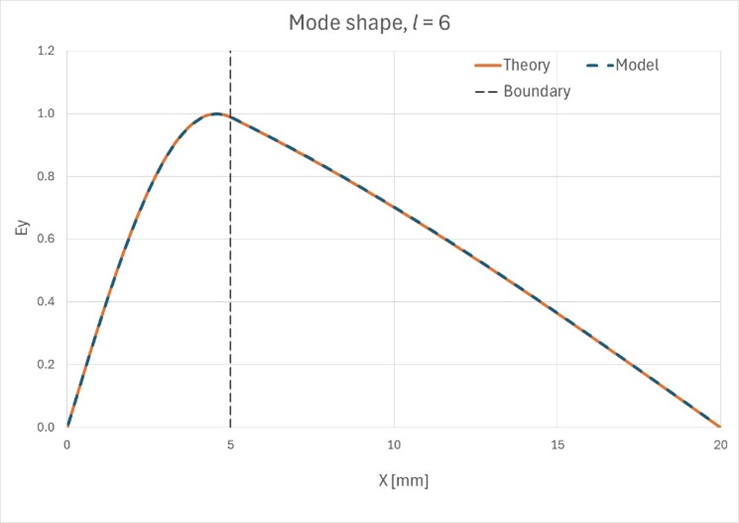
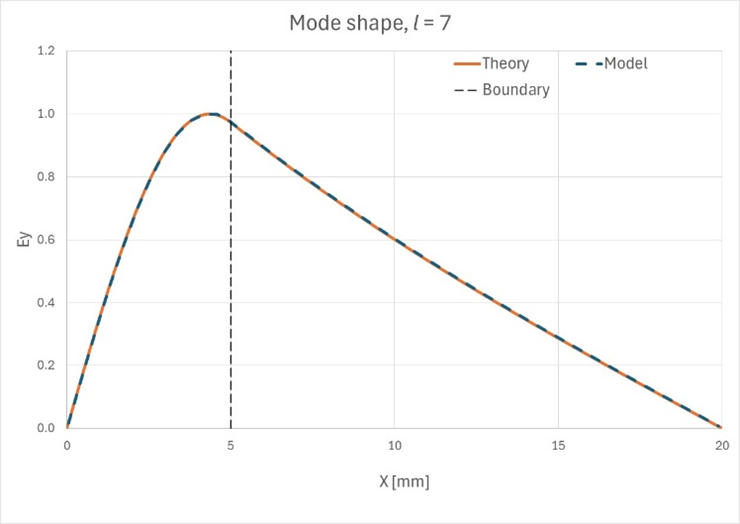
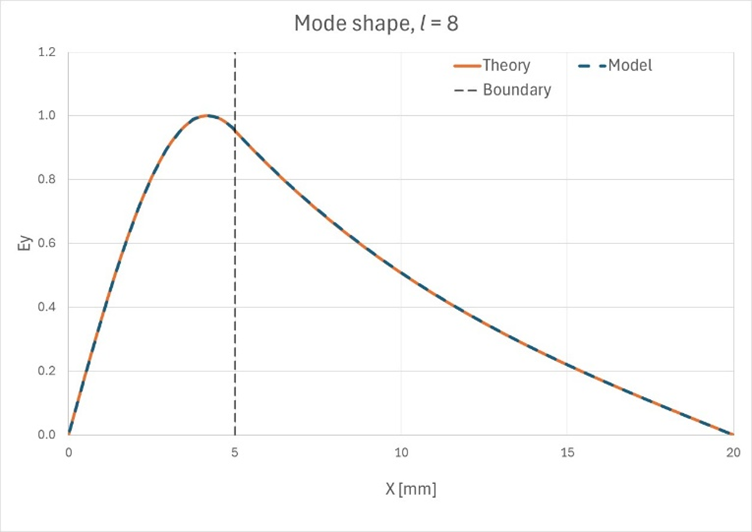
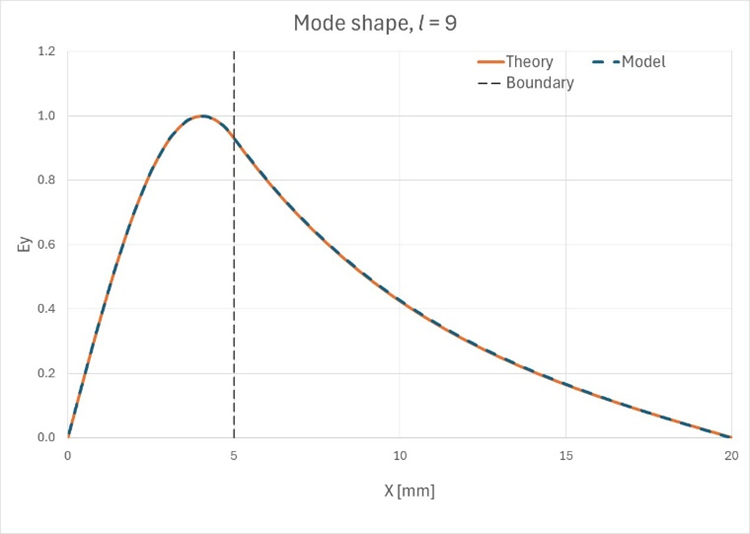
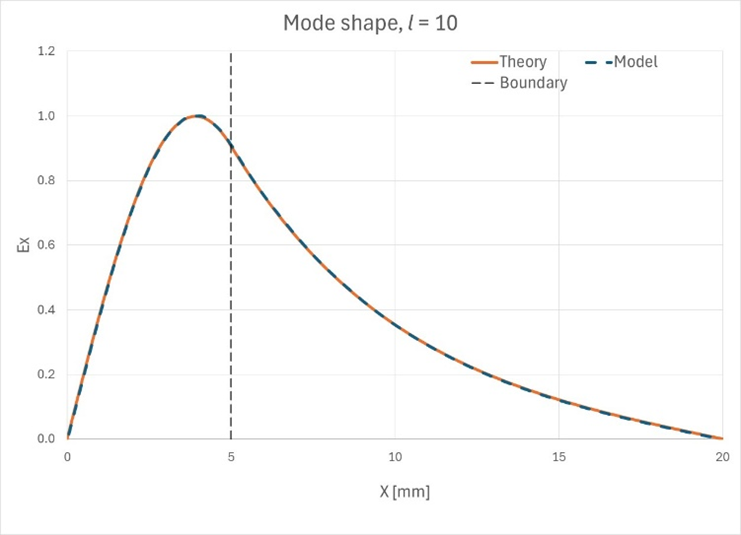
上述したように、あるlの値では境界の両側の解はsin関数で記述され、別の値（私たちのケースではl=7以上）では、空気領域のsin関数は双曲線sinに切り替わります。以下の図で、これを確認できます。
Figure 7. 最初の10の T E 10 l モードのモード形状


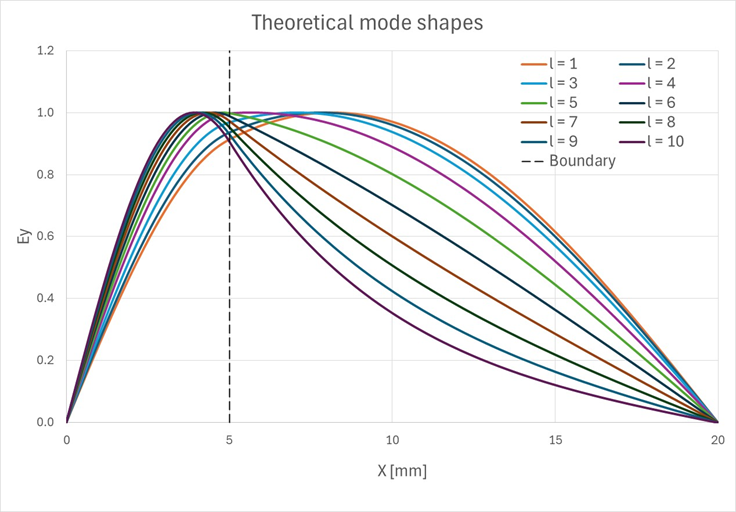
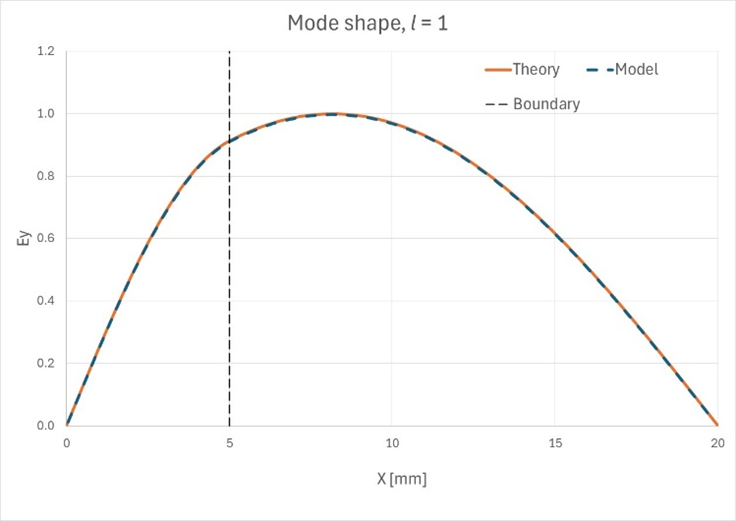
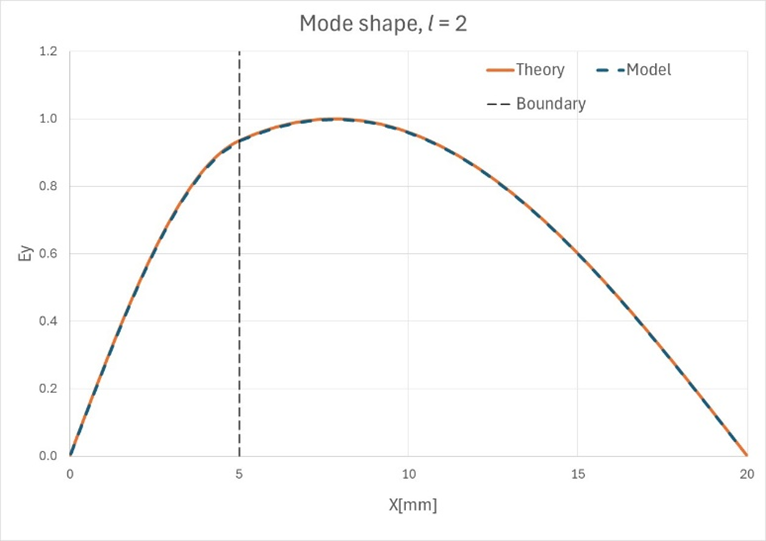
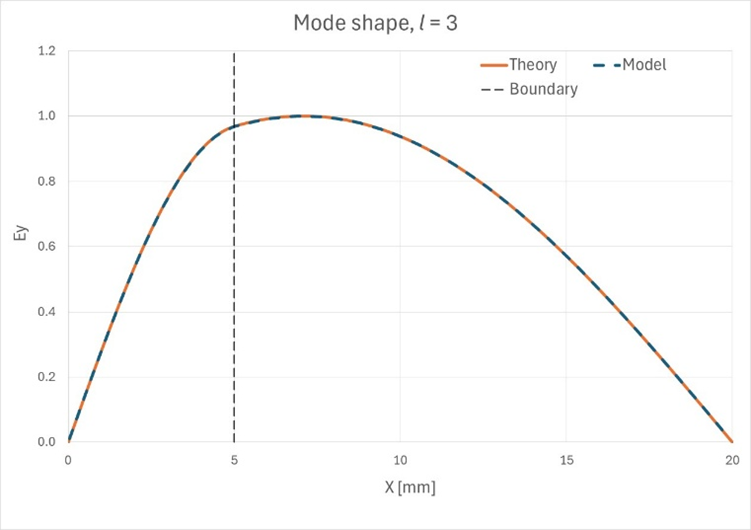
Figure 8. 最初の10の T E 10 l モードの理論上のモード形状と観測されたモード形状が一致

















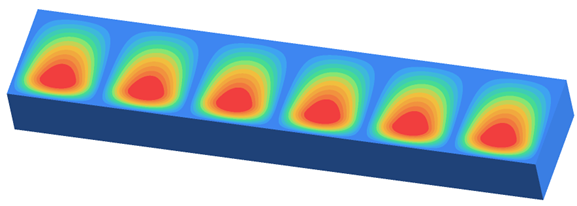
最初の6つのモードは T E 10 l タイプです。モード T E 106 の場の分布を以下に示します。
Figure 9. T E 106 モードの電界強度


y方向に一様でない電界を持つ高次モードは、TE波とTM波の混合です。
Figure 10. モード番号12の電界強度


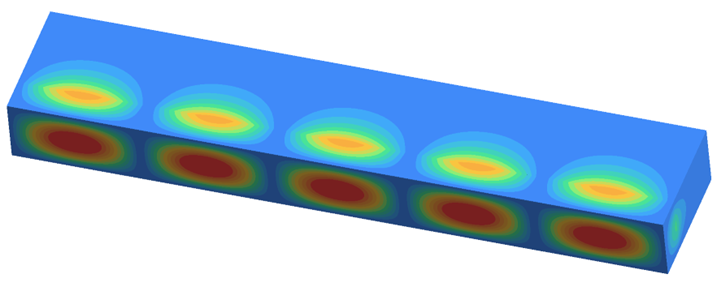
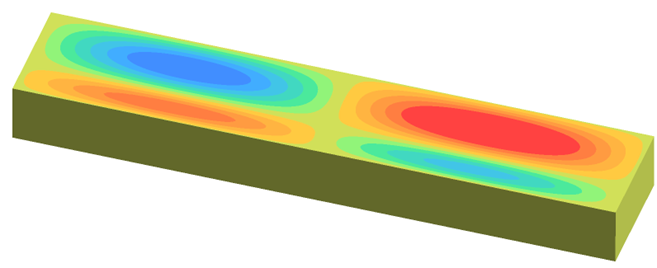
場がy方向に一様な場合、モードはTE波とTM波に分類できます。
Figure 11. T E 202 モードの E y の分布


1 Pozar, D.M., Microwave Engineering, 4th Edition, John Wiley & Sons, Inc., 2012, p.308.